4 Chapter 4: Electrical Properties of Neurons

Austin Lim, PhD (DePaul University)
Editor: Dana Simmons, PhD (University of Chicago)
One of the interesting properties of neurons is that their cell membranes are electroactive, meaning that they are sensitive to electrical charge. Neurons are capable of changing the electrical potential of their membranes, which makes them a very dynamic population of cells. These changes, which can happen on the scale of milliseconds, provide a rapid method for one part of a neuron to send signals over long distances – hence, the analogy of electrical wires running overhead. In this chapter, we will go into depth describing the molecular and cellular components that contribute to the electrical properties of a neuron, both at rest and during an action potential.
Chapter 4 outline
4.1 Ion channels
4.2 The electrochemical gradient
4.3 The Nernst equation
4.4 The action potential
4.5 Movement of action potentials
4.1 Ion channels
The cell membrane that separates the inside of the cell from the outside is a very effective boundary. It is described as being selectively permeable, which means that some molecules are able to travel across the membrane easily, other molecules have an intermediate ability to cross, and other molecules are completely incapable of passing. Generally, gases and molecules of water are able to pass through the cell membrane easily. Large molecules like glucose, and charged molecules like ions or amino acids, are unable to pass across the membrane.
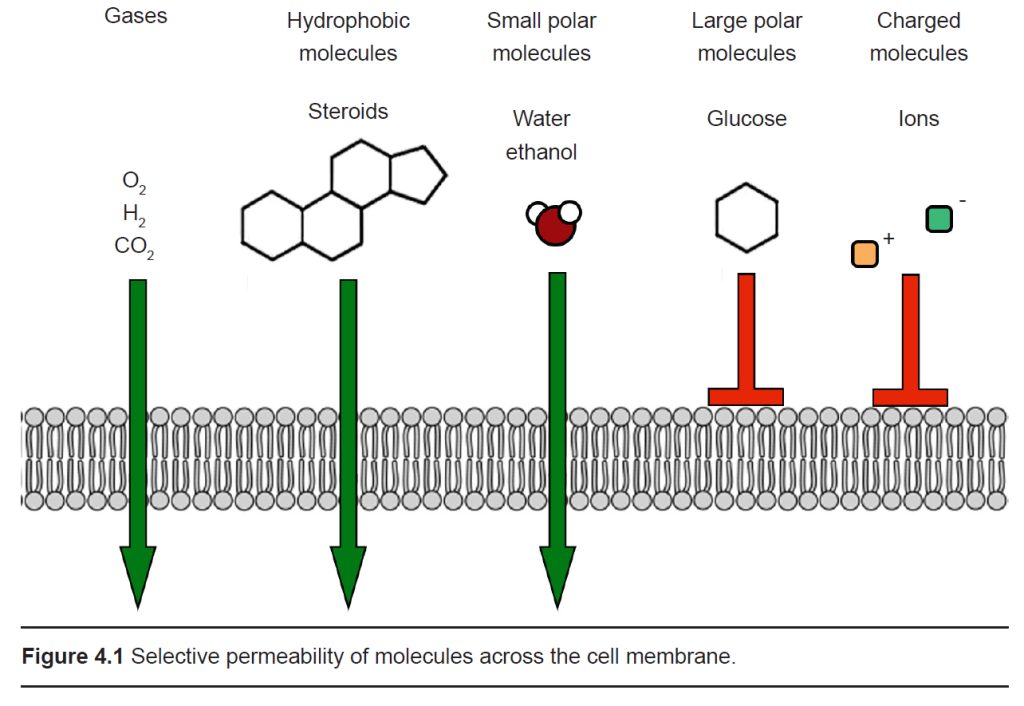
Most cells of the body, including neurons, have specialized transmembrane proteins embedded in the cell membrane. These transmembrane proteins are huge protein complexes that span the entirety of the membrane, with an outer side and an inner side. In the middle of the protein is a pore, which is essentially a tunnel” that allows molecules and ions to pass across the cell membrane. These proteins are called ion channels. These channels are passive since they do not use any cellular energy to move ions. Rather, they simply provide easy passage for ions. It may be useful to think of an ion channel as a “cellular door.”
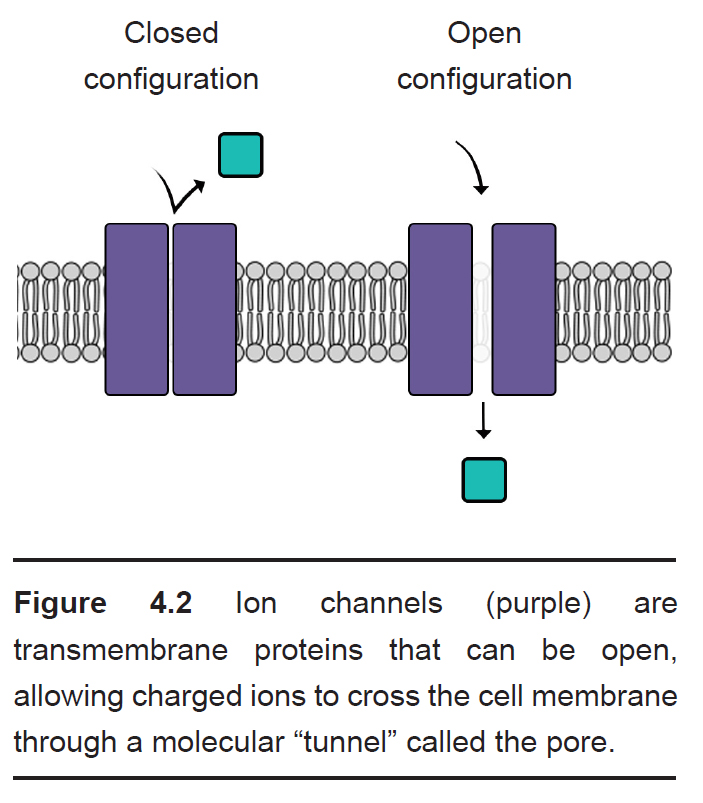
One important feature of ion channels is their ability to distinguish ions based on their chemical properties. For example, some channels are selective for Na+, while preventing the passage of all other ions. Each ion channel has special molecular characteristics that allow certain types of ions to pass through the pore while excluding other ions. Some features that allow for distinction between ions include:
- Pore size. The molecular shape of an ion channel can exclude larger diameter ions if it is small enough, restricting the ability for the large ion to enter the pore – in the same way that a ping pong ball cannot pass through a narrow diameter of a straw.
- Electrical charge. Ion channels can also prevent certain ions from passing through based on the electrical charge. The inside of the pore is lined with charged amino acids, and their charge allows only certain types of ions to pass.
For example, sodium channels have several negatively-charged glutamate residues inside the pore. Because of this, negatively-charged ions like chloride will be repelled by the negative charges, but the positively-charged sodium ions will be attracted to the inside.
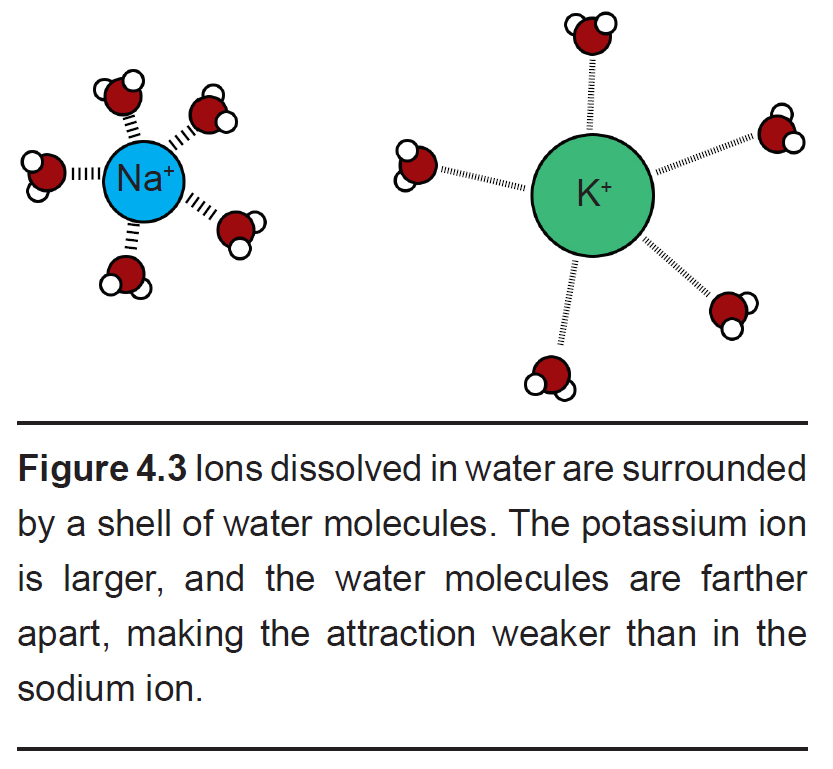
- Hydration shell. Selectivity based on charge and small size is a simple task, but how can it be possible for an ion channel to allow larger ions to pass while excluding smaller ions? This is possible because it is energetically favorable to allow an ion that has been stabilized sufficiently by the properties of the amino acid residues lining the pore.
This process is related to the observation that a shell of water molecules surrounds each charged ion in solution. To pass through the pore, water molecules must be separated from the ion. The potassium ion has diffuse hydration shell, and so it is easier to separate water from a potassium ion compared to a sodium ion. The passage of potassium becomes more energetically favorable compared to passing a sodium ion, causing these pores to be selective.
Like doors, different types of ion channels open and close under different conditions. We can categorize ion channels into four major classes based on their opening and closing conditions.
- Leak channels are persistently open. You can think of these leak channels as revolving doors that are never locked. Neurons usually have several leak channels, such as a leak channel for potassium (K+) and a leak channel for chloride (Cl-) ions. These two ions are at equilibrium, flowing back and forth across the cell membrane, and they help contribute to the properties of the neuron at rest.
- Voltage-gated ion channels are sensitive to the electrical potential of the surrounding membrane. Their ability to open and close depends on the electrical charge of the membrane. Many of them, such as voltage- gated sodium (Na+) channels, remain closed at negative potentials (resting condition) and only open at positive potentials (action potential).
- Ligand-gated ion channels open in response to binding certain molecules (ligands), such as neurotransmitters. These types of ion channels are also called ionotropic receptors, and these will be described in much more depth in chapter 5.
- The fourth class of ion channels is a catch-all category that includes a wide variety of channels that are used by the sensory systems. They open and close in response to unique stimuli depending on what they are able to sense. For example, some open and close depending when they are moved physically, such as a distortion or stretch. We have these in our ears (hair cells, chapter 8.1), in our skin (Pacinian corpuscles, chapter 8.3) and in our muscles (Golgi tendon organ, chapter 10). Photoreceptors in our eyes have ion channels that close in response to being hit by photons of light, and this activity is necessary for us to be able to see in both brightly and dimly lit environments.
4.2 The electrochemical gradient
Without ion channels, ions do not cross the cell membrane and therefore stay either outside or inside the cell. But when an ion channel is present and open, ions can move across the cell membrane, depending on the specific conditions inside and outside the neuron. There are two different forces that act on ions once an ion channel is open: the electrical gradient and the chemical gradient.
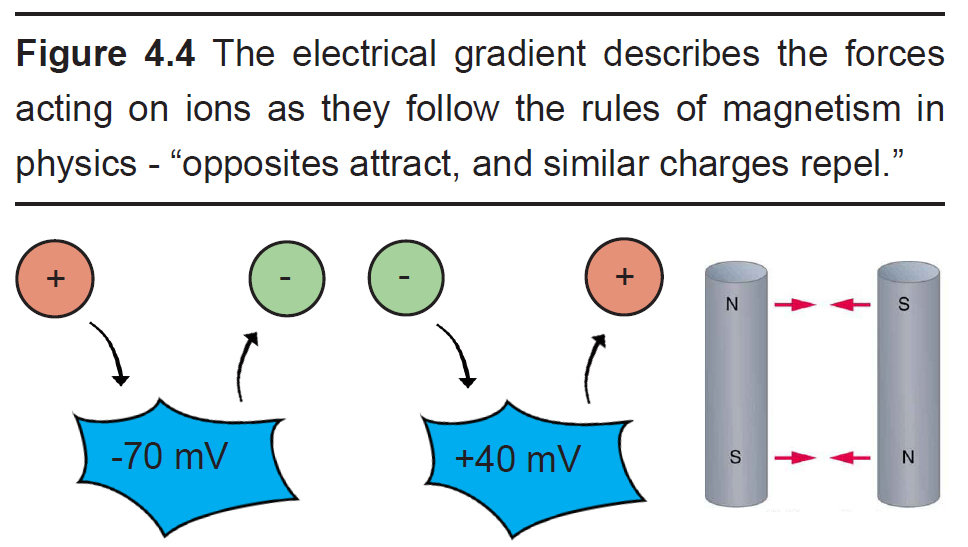
- Electrical gradient
The electrical gradient refers to the electrical forces acting on charged molecules, “pulling” opposite charges together while also “pushing” like charges away from one another – just like the polarity of magnets.
At rest, the interior of the cell has a negative charge, about -70 mV. Because of these negative charges inside the cell, the electrical gradient causes positively charged ions to be attracted to the inside of the cell. At the same time, negatively charged ions will be repelled out of the cell.
The voltage of the neuron (Vm ) can deviate significantly from -70 mV, reaching potentials as high as +40 mV. When the Vm changes, the force exerted by the electrical gradient changes as well. If the cell now has a positive potential instead of a negative potential, movement of charged ions will change as well. In this case, the electrical gradient now attracts negatively charged ions into the cell while pushing positively charged ions out of the cell.
- Chemical gradient
The chemical gradient refers to the natural process by which a high concentration of a substance, given enough time, will eventually diffuse to a lower concentration and settle evenly over the space.
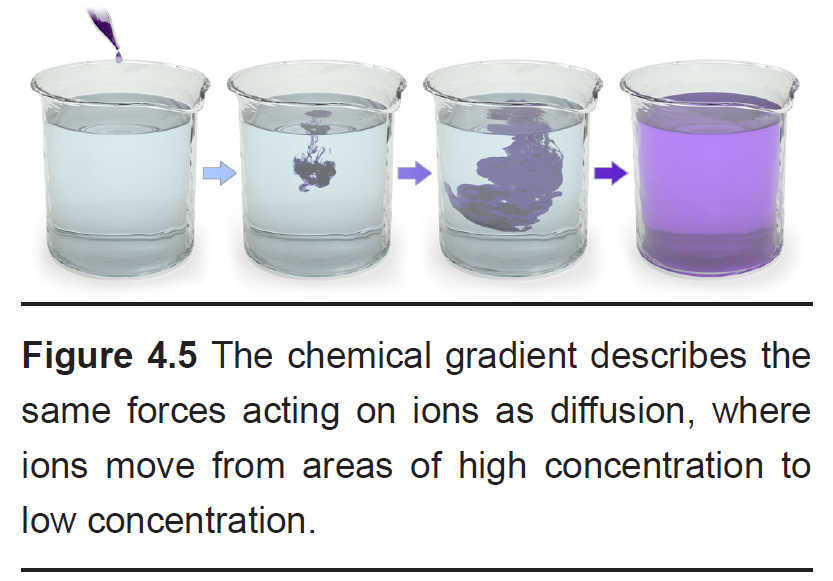
You can think of the chemical gradient as similar to the way people behave when they exit a full elevator. People don’t want to be so close to each other inside a cramped space. Once the doors open, people scatter quickly, going to where they can have more personal space. They move from an area of high concentration to low concentration. Molecules behave the same way.
Unlike the electrical gradient, the chemical gradient is unaffected by biological movement of ions. In other words, the distribution of ions across the membrane does not change significantly. The number of ions that flow across the cell membrane is so minute that the relative distribution of ions across the cell membrane essentially does not change.
These two forces are collectively called the electrochemical gradient. In order to accurately predict the forces acting on a given ion, you need to know 1) the charge of the ion and 2) the relative concentrations of ions across the membrane.
Take a look at the following two examples :
- Sodium (Na+) movement across the membrane
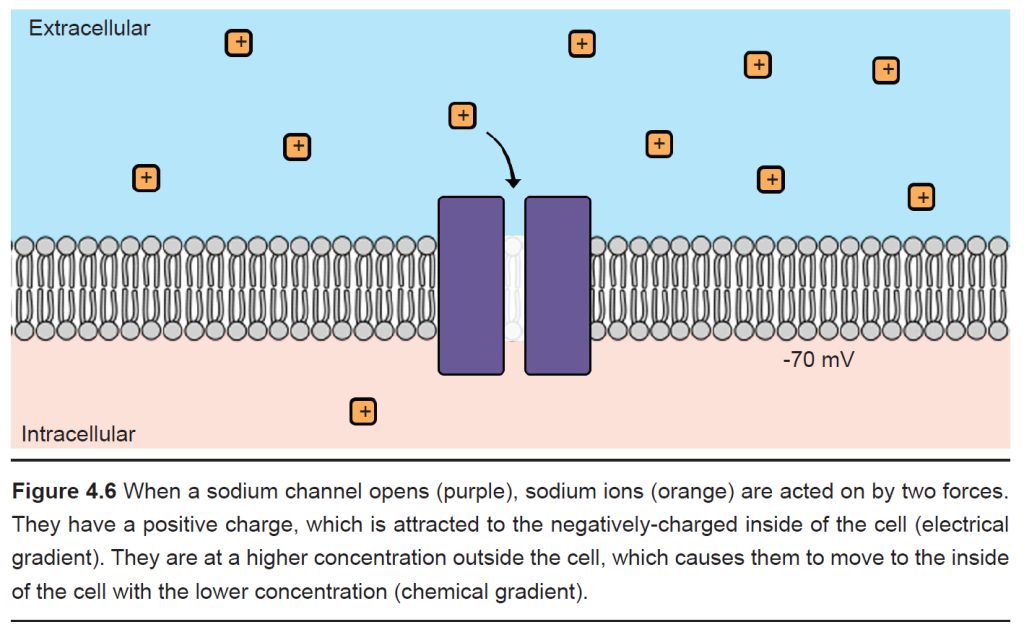
Consider the positively-charged ion, sodium (Na+). Because it has a positive charge, it is electrically attracted to the inside of the cell, which has a negative charge at rest. Therefore, when a sodium-permeable ion channel opens and Na+ is now able to pass across the cell membrane, the electrical gradient causes the sodium to move into the cell.
We also know that the concentration of sodium outside the cell (written as [Na+] , where the brackets indicate concentration and the “o” refers to “outside”) is high compared to the concentration of sodium inside the cell (written as [Na+] ) by roughly an order of magnitude. Therefore, when that sodium-permeable ion channel opens, Na+ will move from the area of high concentration to low concentration, causing Na+ to move into the cell.
Given that both the electrical and chemical gradients are in favor of moving Na+ into the cell, opening a sodium channel causes a net flow of Na+ ions into the cell.
- Potassium (K+) movement across the membrane
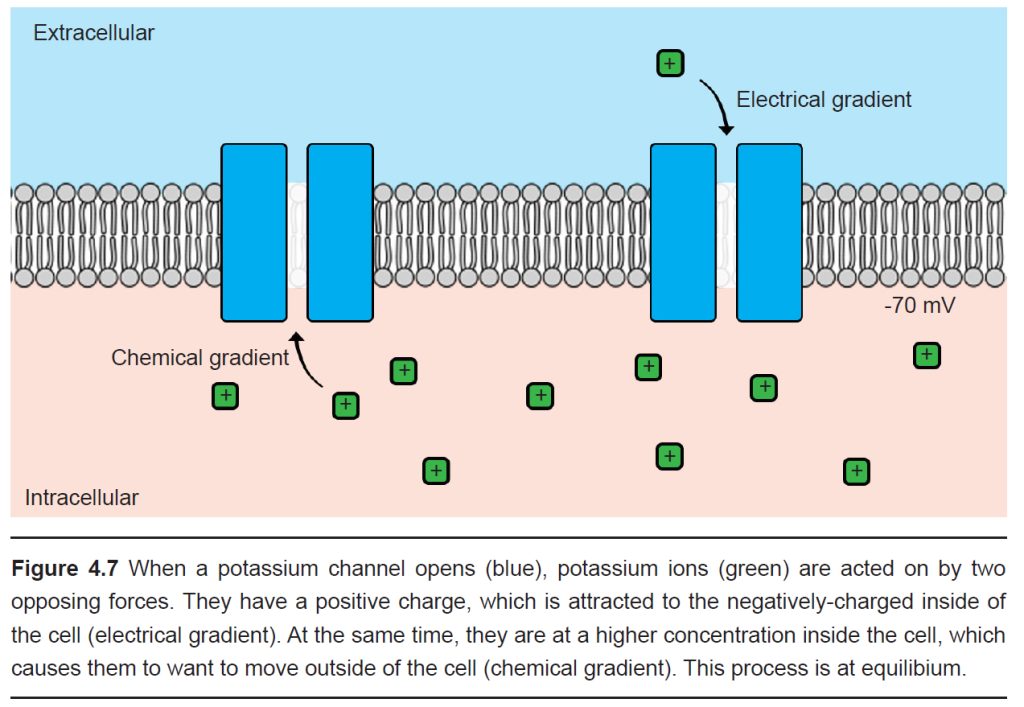
Just like with sodium, we can use our knowledge of potassium’s charge and the distribution of K+ ions across the membrane in order to predict the forces acting on K+ ions when a potassium channel is open.
We know that the inside of the cell is negative and K+ has a positive charge, so the electrical gradient causes K+ to be attracted into the cell. We also know that the inside of the cell has a relatively high concentration of K+ ions compared to the outside of the cell; therefore the chemical gradient pushes K+ out of the cell.
Since the ion concentrations across the membrane do not change significantly, but the membrane voltage can, you could imagine there exists some Vm where the flow of ions moving in are exactly equal to the flow of ions moving out. In this case, the two forces acting on the ion oppose one another perfectly, resulting in a dynamic equilibrium (This process is called “dynamic” because there is a constant movement of ions going in and going out, and yet it is at an “equilibrium” because there is no net movement of charge: the charge moving in is balanced by the charge moving out.) This exact value of the Vm is called the equilibrium potential for the ion, which is also abbreviated Ex where x is the ion of interest. The equilibrium potential differs for each ion, and is described in Table 4.1.
Could we update spelling of equilibrium in caption?
| Ion | Abbreviation | Concentration outside [X]o | Concentration inside [X]i |
| Sodium | Na+ | 140 mM | 15 mM |
| Potassium | K+ | 5 mM | 150 mM |
| Chloride | Cl- | 120 mM | 10 mM |
| Calcium | Ca2+ | 1 mM | 100 nM = 0.1 µM |
| Magnesium | Mg2+ | 2 mM | 0.5 mM |
| Miscellaneous anions | A- | 20 mM | 100 mM |
Table 4.8 Charged ions are unequally distributed across the cell membrane. Typical concentrations of ions in a mammalian neuron.
4.3 Calculating Ex and the Nernst equation
Even though the equilibrium potential (Ex) for each ion can be determined experimentally, it is also possible to calculate Ex using a mathematical equation called the Nernst equation. By understanding the Nernst equation, you can predict the direction that ions will move when an ion channel opens given various conditions. The Nernst equation is as follows:
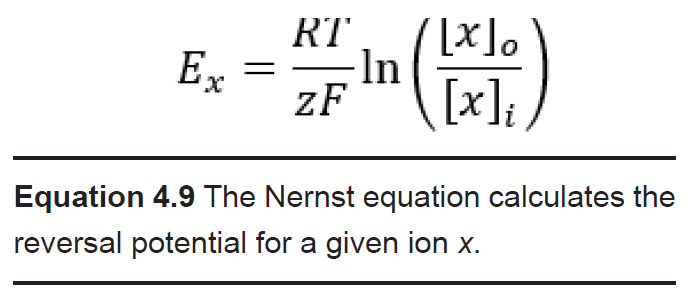
Ex is the equilibrium potential. As a potential, it has units in volts, usually measured in millivolts. When a cell’s membrane potential is exactly at this Ex, the ion is at equilibrium: ion movement into the cell is matched by ion movement out of the cell. Ex is sometimes also called the reversal potential, because once the cell membrane crosses from this potential, the net movement of the ions reverses directions. This value is also called the Nernst potential in honor of Walther Nernst, the Nobel prize-winning German chemist who first developed the formula to describe electrochemical reactions.
R is the ideal gas constant. It has a value of 8.314 J / K * mol. The R term is included in the equation because it is a way to convert between the number of molecules and the energy that these molecules exert.
T is the temperature in Kelvin (to convert from Celsius into Kelvin, add 273 to the Celsius value. C + 273 = K). Usually, room temperature is around 293 K, and biological temperatures are closer to 310 K. This term is included in the equation since all biological processes are temperature dependent, especially those at the level of molecular machinery.
z is the electrical charge of the ion. For sodium and potassium, z is +1, for chloride or monovalent anions z is -1, and for divalent cations like calcium and magnesium, z is +2. This term is essential since the Nernst potential is used to predict the direction of ion movement based on the charge of the ion. This value represents the influence exerted by the electrical gradient.
F is the Faraday constant which has a value of 96,485 Coulombs / mol.
[x]o and [x]i represent the concentration of ion x outside the cell and inside the cell, respectively. Their units are generally in mM, but these units cancel out in the equation. These values represent the forces acting on the ions by the chemical gradient.
The Nernst equation has many complex constants and terms, so neuroscientists often use the back-of-the-envelope equation as a shortcut for quickly calculating the equilibrium potential. This shortcut equation condenses down the R and F constants, turns the natural log into a base 10 logarithm, and assumes the calculations are done at physiological temperature. The shortcut formula can be written as:
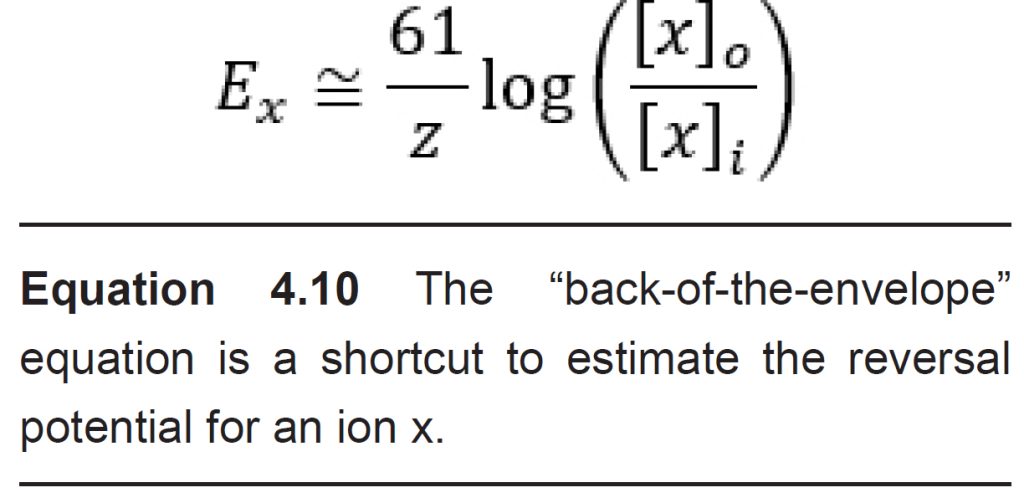
The Nernst equation can be used to calculate the reversal potential for individual ions assuming that the appropriate ion channels are open. However, in neurons, not all ion channels are opened or closed at the same time. In a neuron at rest, usually Na+ does not enter into the cells since sodium channels are closed. K+ ions , on the other hand, are often moving through leak channels all the time. Chloride channels are generally open as well, but they pass less current at rest than potassium channels do.
A formula called the Goldman-Hodgkin- Katz equation (GHK equation) combines the Nernst potentials of three relevant ions (Na+, K+, and Cl-) into a single equation that, when evaluated, gives us the value of the membrane potential, Vm.
The GHK equation is written as:

When you analyze the GHK equation, you will notice that it is essentially a combination of the Nernst equations for the equilibrium potentials for the three ions. The GHK equation also introduces a new term, the value p which stands for permeability: the ability for an ion to cross the membrane through ion channels. Permeability itself does not have a unit.
It is easier to think of permeability as the “weight” of each equilibrium potential. The higher the permeability for a given ion, the closer the Vm is to the Ex for that ion. For example, consider the value of the GHK equation for neurons at rest.
Under these conditions, the permeability for K+ (pK) is 1, pCl is 0.55, and pNa is 0.04. Therefore, the resting membrane potential Vm will be closest to a combination of EK and ECl, since these two terms dominate the GHK equation. Just as a reminder, the resting membrane potential is around -70 mV, and EK is around -80 mV while ECl is around -60 mV.
However, during an action potential (described in section 4.4), permeability for sodium increases significantly. As pNa rises, the membrane potential will shift closer towards ENa, which is +55 mV. The GHK equation provides a mathematical explanation for how movement of Na+ across the membrane causes the cell to become more positive.
4.4 The action potential
The action potential is a short-lasting (1 or 2 milliseconds), temporary change in membrane potential that can travel down the length of the axon. Action potentials are the main method of communication that neurons use, and each action potential triggers the release of neurotransmitters at the axon terminal of a chemical synapse. Action potentials are all-or- nothing responses, meaning that only a large change in potential will be able to pass the signal forward, but a small, sub-threshold change in Vm will not. Sub-threshold changes in Vm are called graded potentials.
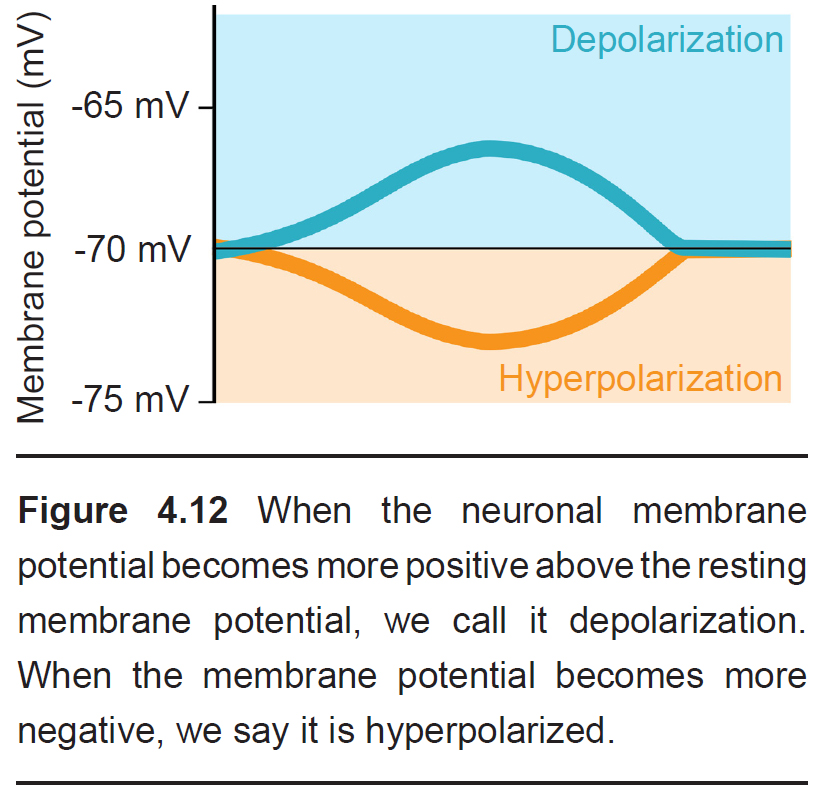
During an action potential, the membrane potential deviates from the resting membrane potential of around -70 mV (this value can range from -90 mV to -50 mV, depending on the type of neuron) to positive potentials. When Vm goes from negative to a more positive potential, this change is described as a depolarization. Likewise, when Vm changes to a value that is more negative, it is called a hyperpolarization. The action potential has a very characteristic shape: a rapid depolarization, followed by a prolonged hyperpolarization, before repolarizing and slowly returning to the resting membrane potential over the next few milliseconds.
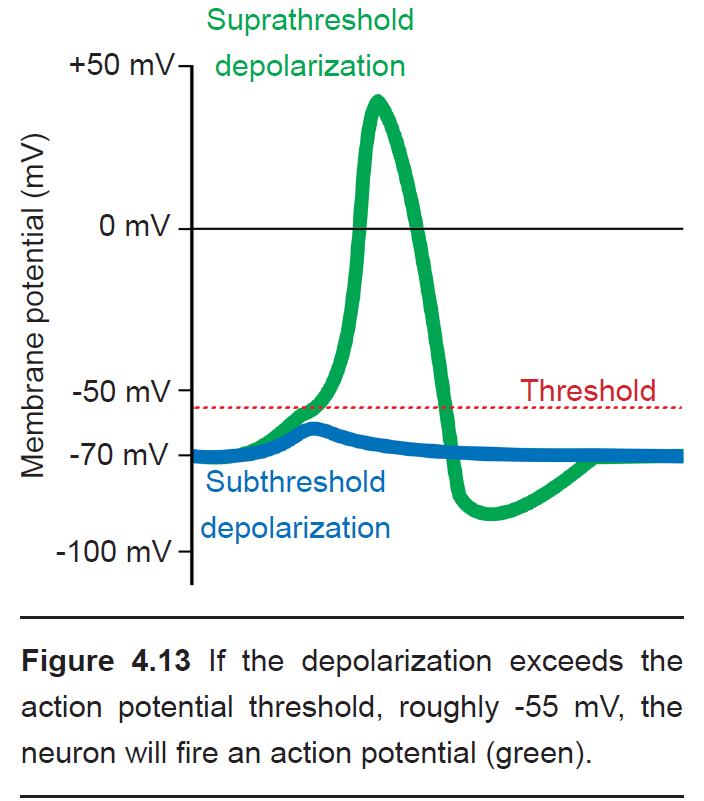
Cells regularly receive many inputs at once. To trigger an action potential, the sum of the inputs must be sufficiently depolarizing to bring the Vm to a value that is more positive than the action potential threshold. For an average neuron, the action potential threshold is around -55 mV. Anything less than the action potential threshold will fail to send the signal forward.
The change in membrane potential seen in an action potential is driven by the movement of ions, predominantly sodium and potassium, across the cell membrane through voltage-gated ion channels. An action potential takes place in 5 steps, some of which overlap in duration.
-
Depolarization from incoming neurons
Presynaptic neurons that release neurotransmitters onto dendrites cause a small amount of ion movement via postsynaptic ligand- gated ion channels. These small deviations in membrane voltage are called postsynaptic potentials, or PSPs. Release of excitatory neurotransmitters causes small depolarizations which are called excitatory post synaptic potentials (EPSPs), while release of inhibitory neurotransmitters cause small hyperpolarizations, or inhibitory post synaptic potentials (IPSPs). These PSPs are characterized by a fast but small rising phase where the Vm changes quickly followed by a slower decay phase where the Vm resets back to resting potential.
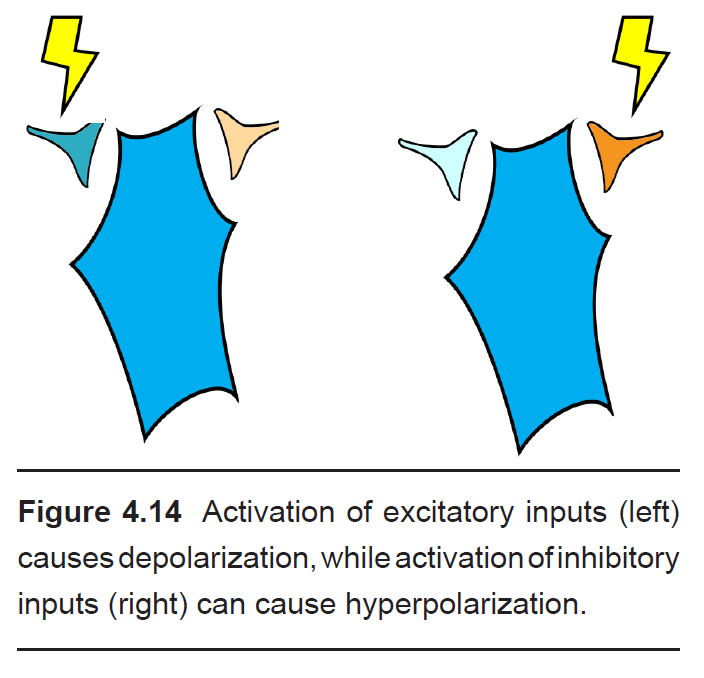
Usually, a single EPSP only causes a small amount of depolarization that isn’t sufficient for bringing Vm above the threshold potential. Reaching the threshold often requires multiple EPSPs. Multiple EPSPs are added together in one of two ways: spatial summation and temporal summation. Spatial summation happens when two small EPSPs from two adjacent inputs are triggered. Temporal summation occurs when multiple EPSPs from the same input occur close together in time. Each individual EPSP has a normal decay period, and adding a second EPSP during that decay period causes the two to add together, which may now be large enough to bring Vm above the action potential threshold. When a large enough total depolarization of membrane potential reaches the soma, an action potential is initiated at the axon hillock.
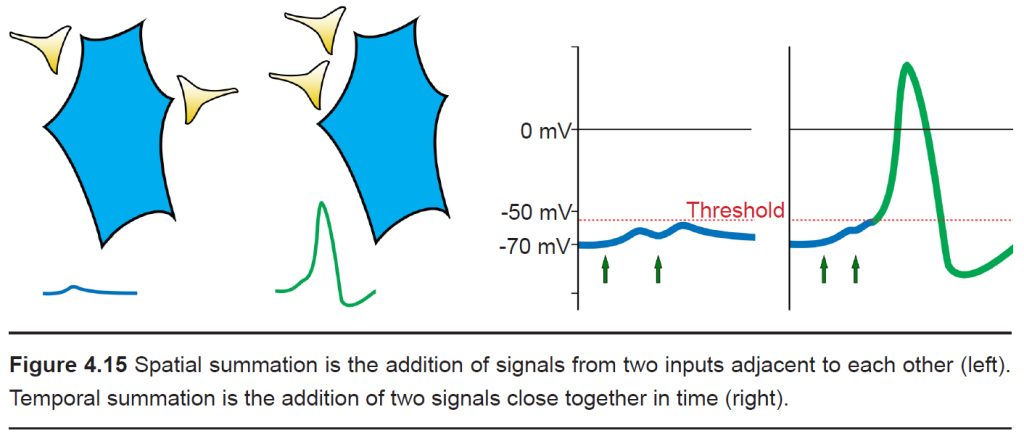
-
Opening of voltage-gated Na+ channels
At rest, the voltage-gated ion channels are
almost all closed. But as the Vm depolarizes, the channels are more likely to open. At this point, we use our understanding of the electrochemical gradient to predict the movement of Na+ ions. The positively charged sodium ions are drawn to the negative potential on the inside of the cell, and the ions move from the area of high concentration (outside the cell) to an area of lower concentration (inside the cell). Both forces are in favor of Na+ entering the cell when the voltage- gated sodium channels open, and this movement of positive charges into the cell causes further depolarization.
Na+ movement across the cell membrane into the cell causes the Vm to depolarize to very positive potentials. The peak of the action potential can reach +40 mV.
-
Opening of voltage-gated K+ channels
Embedded in the cell membranes are other voltage-gated channels that are selective for K+ rather than Na+. Like the voltage-gated Na+ channels, these K+ channels begin to open when the cell starts to depolarize, allowing K+ ions to move across the cell membrane.
When the cell has depolarized to about +40 mV, we can use our knowledge of the electrochemical gradient to make predictions about what happens to K+ ions. The positive potential inside the neuron repels the K+ ions (electrical gradient), and the relatively high concentration of K+ inside the cell pushes K+ out of the cell (chemical gradient). In total, both of these forces act on the K+ ions to leave the neuron. Movement of positive charge carriers out of the cell makes the interior of the cell (and Vm) more negative. K+ movement through the voltage-gated potassium channels causes the cells to become more negative than the resting membrane potential.
-
Inactivation of voltage- gated Na+ channels
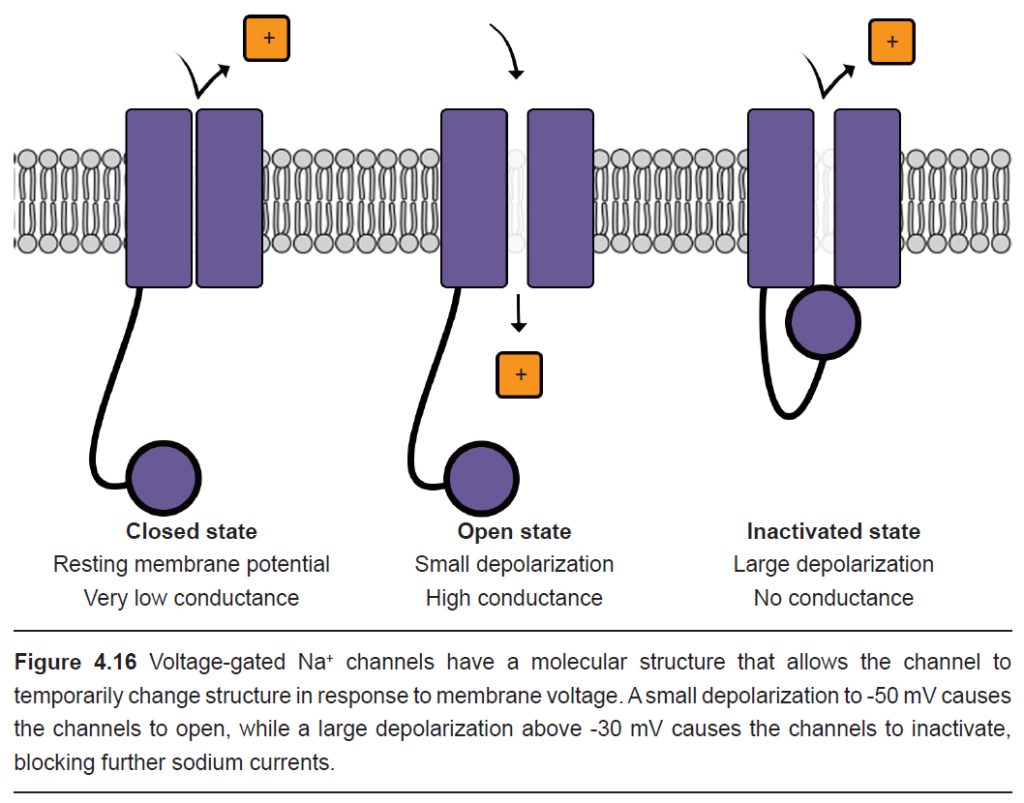
Voltage-gated Na+ channels have a very complex molecular structure. In addition to having a pore through which ions can move across the cell membrane, they have an inactivation gate that can block the flow of sodium ions. When the cell membrane reaches a positive potential, the inactivation gate closes, thus preventing further movement of excitatory, depolarizing Na+ ions.
These voltage-gated Na+ channels undergo the inactivation process very rapidly, often times faster than a millisecond.
-
Deactivation of voltage-gated K+ channels
In this last step of the action potential, the main current flow is an outward current as the positively-charged K+ ions are driven out of the cell through voltage-gated K+ channels by the electrochemical gradient. When positive charges leave the cell, the interior once again becomes more negative.
Unlike the voltage-gated Na+ channels, the process of deactivation is much slower. On average, it may take these channels a few milliseconds to deactivate.
When these K+ channels deactivate, the hyperpolarizing current stops, which causes the membrane potential to gradually return to the equilibrium of resting potential.
Clinical connection: Chronic pain
Nociception is a complex sensation that the nervous system detects rapidly. Pain is the perception that the body is experiencing some kind of injury or noxious stimulus, so pain triggers a reflex that causes the person to withdraw from the painful stimulus, which decreases the severity of the damage. Pain can also create memories that discourage people from future contact with pain-inducing situations.
When we experience a noxious stimulus, that information is sent towards the central nervous system by means of action potentials. And in most cases, the detection of pain is a healthy, protective sensation.
There are, however, some people with a dysregulation in their somatosensory systems that cause them to experience pain even in the absence of injurious stimuli, a condition called allodynia. Although we still don’t understand what causes allodynia, it is known that some change in voltage-gated sodium channel properties causes an increase of excitability of pain-sensing neurons is increased.
In summary, you can also think of the shape of the action potential as consisting of three phases.
- Depolarization. The upwards deflection (-70 mV to +40mV) of the action potential that lasts for half a millisecond. Vm becomes more positive because of Na+ ions that enter the cell through the voltage-gated sodium channels. At this step, the voltage-gated potassium channels also start to open.
- Repolarization. The rapid downwards deflection (+40 mV to -70 mV), also lasting for about half a millisecond. Here, the voltage-gated sodium channels have almost all inactivated, and positively-charged K+ ions are being driven out of the cell through the voltage-gated potassium channels. As positive charges leave the cell, Vm becomes more negative.
- Afterhyperpolarization. The slow return back to the resting membrane potential (-70 mV to -80 mV and back to -70 mV ) that can last for a few milliseconds. This return back to the equilibrium of the resting state is due to the gradual deactivation of voltage-gated potassium channels.
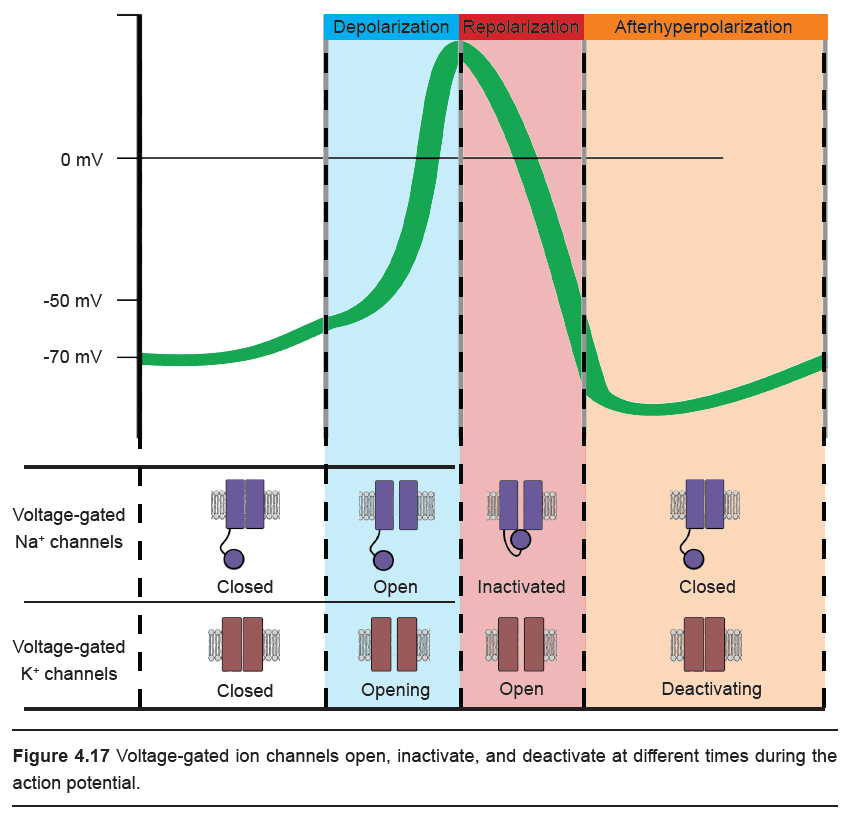
Ions moving across the membrane change the membrane potential. The best way to think about the change in Vm in response to ion movement is to consider the equilibrium potential of each individual ion that is moving. For example, ENa is +55 mV. When a voltage- gated sodium channel opens and Na+ ions are able to move across the cell membrane, the membrane potential shifts towards ENa, which is a depolarization. During the repolarization phase, when the voltage-gated K+ channels open, the potential across the cell membrane now shifts towards the equilibrium potential for K+, which is close to -80 mV.
The steps of the action potential can also be thought of in mathematical terms by examining the variables of the GHK equation. As permeability for a given ion increases, it shifts the balance of Vm more heavily towards the equilibrium potential of that specific ion. So, during the depolarization phase of the action potential when the voltage-gated sodium channels open, the permeability term for sodium (pNa) increases to as high as 20, which causes Vm to move towards ENa (+55 mV). And during the repolarization phase, voltage- gated potassium channels open, while the voltage-gated sodium channels are inactived. When this happens, pK increases, pNa drops to zero, and as a result, the Vm shifts towards the equilibrium potential for potassium (-80 mV).
Randomness in ion channel properties
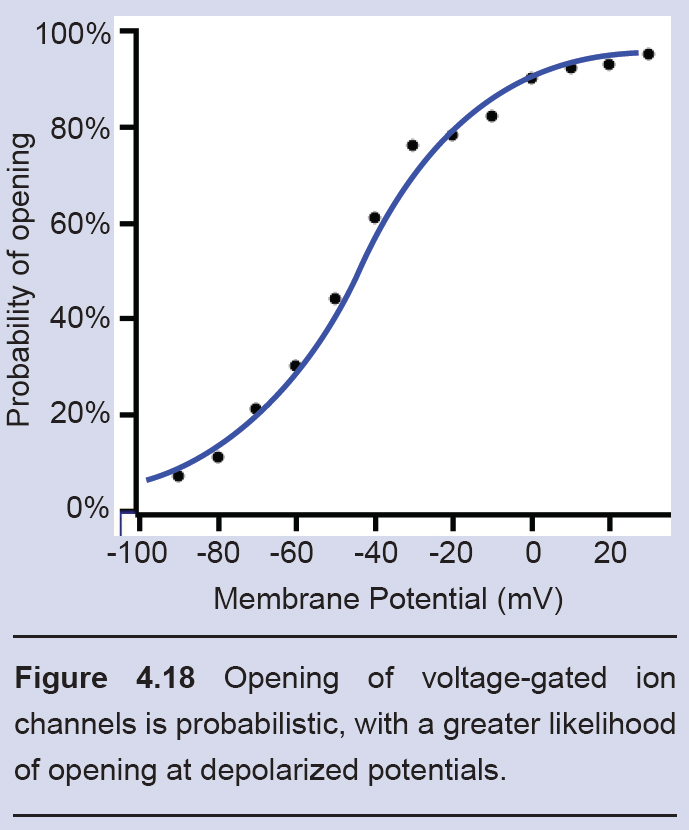
Voltage-gated ion channels do not follow a precise “if-then” flowchart in determining when to open, inactivate, or deactivate. Rather, ion channels are very probabilistic in nature. For example, consider as a voltage-gated sodium channel changes from the closed state to the open state. A single channel like this might show probabilistic behavior as follows: at -70 mV, there is a 0.1% chance to open. At -30 mV, there is now a 50% chance to open. At +20 mV, there is a 99.9% chance to transition to the open configuration.
Likewise, these channels also transition from the open state to the inactive state on a probabilistic basis as well, with the greatest probability of inactivating at depolarized potentials.
In the moments following the beginning of an action potential, there is a time window where a second action potential cannot be fired. This time window, about half a millisecond in duration, is called the absolute refractory period. On a molecular level, the absolute refractory period exists because the voltage- gated sodium channels are inactivated, which prevents them from being able to pass any more inward excitatory current. The absolute refractory period may last for up to a millisecond.
A few milliseconds after the end of the absolute refractory period begins a phase called the relative refractory period. During this phase, it is more difficult to fire an action potential compared to the resting condition. At the level of the receptors, the relative refractory period exists for two main reasons. First, only some of the voltage-gated sodium channels have “reset” from their inactive state. Second, many of the voltage- gated potassium channels are still in the open state, which allows the movement of K+ ions, causing the neuron to rest at a more negative potential. Also, increased movement of K+ ions hinders depolarization, as the GHK equation demonstrates, since potassium movement pulls membrane potential closer towards the equilibrium potential for K+. This relative refractory period lasts as long as the afterhyperpolarization and, therefore, exists on a gradient: the sooner after the repolarization phase of the first action potential, the more difficult it will be to reach threshold for a second action potential.
4.5 Movement of the action potential
Up to this point, we have only considered a single piece of cell membrane and how it responds during an action potential. For an action potential to travel from the axon hillock to the axon terminal, this temporary change in Vm must physically move down the length of the axon. The ability for the action potential to travel is made possible because the Na+ ions that enter through voltage-gated sodium channels are not restricted to the cytoplasmic volume beneath the ion channels. These Na+ ions behave just like any other substances that are in an area of high concentration: they move towards areas of low concentration. As Na+ rushes into the cell, they follow the chemical gradient and quickly move toward areas of low concentration, which is the next section of membrane. When they do so, the next patch of the membrane becomes depolarized. This depolarization causes the next set of channels to open, which results in even more sodium influx. From here, the process repeats down the axon. The action potential is a chain reaction that starts at the axon hillock and doesn’t stop until the axon terminal.
An action potential is like a wave. It only moves in one direction, and there are two main reasons why:
- First, sodium ions move down their concentration gradient. The Na+ ions that enter through a voltage-gated sodium channel are less likely to want to move in the reverse direction, since this area currently has a relatively high Na+ concentration. Instead, they will move towards the area with a low concentration of ions, which is the forward direction.
- Secondly, the previous patch of membrane is in the absolute refractory period, which makes it impossible for an action potential to travel backwards. During this time, many voltage- gated sodium channels are still inactivated, and most voltage-gated potassium channels are open.
Analgesia and motor signaling
A trip to the dental office sometimes requires an injection of an analgesic like lidocaine before the dentist performs any otherwise-painful procedures. On a molecular scale, lidocaine is an inhibitor of voltage-gated sodium channels. By blocking these channels, lidocaine prevents action potentials from traveling up the afferent pathway, preventing incoming sensory inputs from the teeth and gums from reaching the central nervous system. When these signals are blocked, we don’t feel any drilling.
Just as incoming signals can be inhibited through voltage-gated sodium channel inhibitors, so can outbound signals – sometimes with deadly consequences. Through evolution, nature came across a variety of voltage-gated sodium channel inhibitors that function as poisons to prevent predation. Because the efferent pathway is used to signal components of the motor system, blocking downward signals can lead to paralysis. One family of fish, the pufferfish, may have a very high concentration of a deadly voltage-gated sodium channel inhibitor called tetrodotoxin, or TTX. This toxin is produced by a bacteria that live symbiotically in pufferfish organs. Ingestion of TTX prevents neurons from communicating. One efferent signaling pathway, the phrenic nerve, signals the diaphragm to move up and down. Without proper medical treatment, people exposed to doses as small as 1 milligram of TTX can die of respiratory failure in hours.

Despite these tremendous risks, pufferfish is a delicacy in Japan. The dish, called fugu, can cause numbness of the lips and even a mild intoxication.
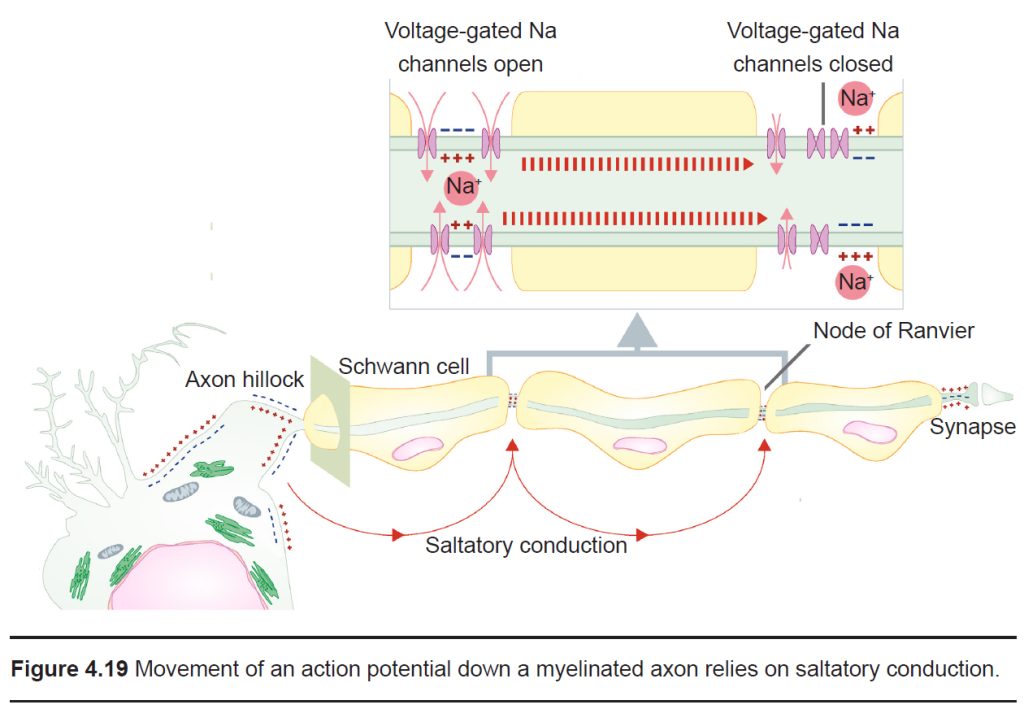
The role of myelin
Previously, in discussing the cellular anatomy of the neurons, we described myelin, layers of lipid that are sometimes thickly wrapped around the axon of the neuron. Myelin increases conduction velocity, the speed at which an action potential travels down the length of the axon. Myelin works by physically blocking leak potassium channels in the cell membrane. By covering these channels, positive charges become unable to exit the cell, which causes the signal to move more rapidly.
A myelinated axon still requires some influx of sodium ions for the signal to travel, however. This influx occurs at the nodes of Ranvier, the unmyelinated segments of the axon. These areas are very dense with voltage- gated sodium channels. Because the changes in electrical charge are detected at intervals, we sometimes say that the signal is passed by saltatory conduction (saltare is the Italian word for “jump”).
In this chapter, we described the molecular and cellular underpinnings of the action potential, the main method of signaling that the nervous system uses for communication. In the following chapter, we will explain how neurons talk to one another using those electrical signals in combination with chemical signals called neurotransmitters.
Image Credits
Title page: Image by pasja1000 from Pixabay, Image by TeroVesalainen from Pixabay
4.4. OpenStax / CC BY (https://creativecommons.org/licenses/by/4.0) https://commons.wikimedia.org/ wiki/File:Openstax_college-physics_22.5_magnet-pole-attraction.jpg
4.5 (diffusion fig BruceBlaus [CC BY 3.0 (https://creativecommons.org/licenses/by/3.0)]
4.18 Correa AM, Bezanilla F. Gating of the squid sodium channel at positive potentials: II. Single channels reveal two open states. Biophys J. 1994 Jun;66(6):1864-78. doi: 10.1016/S0006-3495(94)80980-4. PMID: 8075324; PMCID: PMC1275912.
4.19 https://commons.wikimedia.org/wiki/File:Propagation_of_action_potential_along_myelinated_nerve_fiber_en.svg modified by Austin Lim
4.20 https://upload.wikimedia.org/wikipedia/commons/4/4e/Pufferfish_%28Butete%29.jpg
The Open Neuroscience Initiative is funded by a grant from the Vincentian Endowment Fund of DePaul University.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

